Evaluation, Intelligence

Where might better ratings come from?

June 23, 2019 — 0 Comments

Evaluation, Intelligence, Reasoning, Tradecraft

What might an alternative to the ODNI Rating Scale be like?

May 24, 2019 — 0 Comments

Evaluation, Expertise, Intelligence, Tradecraft

The ODNI Rating Scale – Issues Abound

May 19, 2019 — 3 Comments

Espionage, Intelligence

A revolution in spycraft?

April 28, 2019 — 0 Comments

Citizen Intelligence, Crowdsourcing, Intelligence

Challenges in getting a citizen intelligence marketplace up and running

April 15, 2019 — 0 Comments

Citizen Intelligence, Crowdsourcing, Intelligence

A challenge model for citizen intelligence

April 14, 2019 — 0 Comments

Citizen Intelligence, Intelligence

Citizen intelligence lacks a marketplace

April 13, 2019 — 0 Comments

Intelligence, Prediction, Teams

Three new papers relevant to improving analysis

April 11, 2019 — 0 Comments

Citizen Intelligence, Intelligence

Citizen Intelligence is fast becoming a real thing

April 10, 2019 — 1 Comment

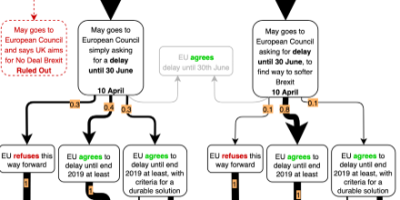
Forecasting, Intelligence, Visualization

A Worthy approach to complex & uncertain futures

April 8, 2019 — 0 Comments